A Levelled Mentorship Approach to Genetic Algorithms for the Travelling Salesman Problem
A novel approach to using genetic algorithms to solve the travelling salesman problem
Firstly, I know that title is a mouthful but trust that it'll be very clear by the end of this. In this blog post I will talk about how I used a unique approach in the genetic algorithm process to increase the effectiveness of the "basic" algorithm that I learned from Tom Mitchel's Machine Learning book and how I applied it to the Travelling Salesman Problem.
Here is a link to the more technical paper I wrote on this project and a link to the Github Repo with the source code for those interested.
Levelled Mentorship Approach for TSP Paper
GitHub Repo Source Code
The Travelling Salesman Problem (TSP)
The Travelling Salesman Problem is a straight-forward way of representing a graph problem. It asks the question, "If you have a list of cities and the distance between each pair of cities, what is the shortest path you can take that will visit all the cities exactly once and return to the city you started from." Now I used the world cities but this can mean nodes or any replacement and distance could be a cost to go from node A to B.
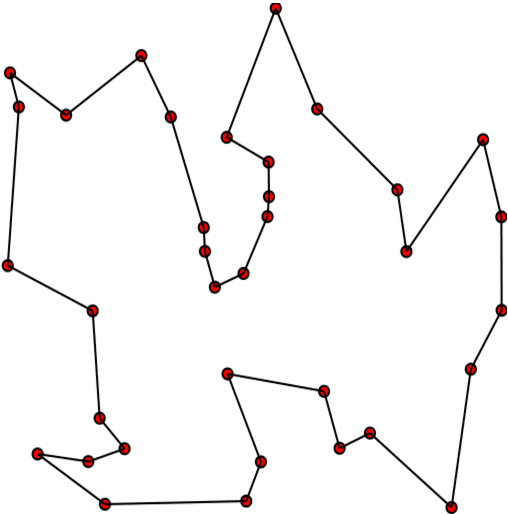
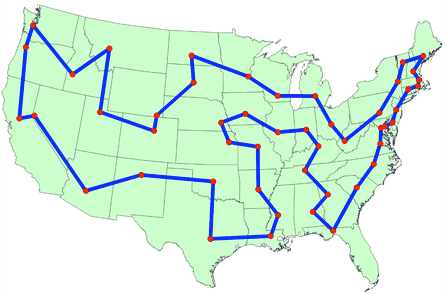
Have you ever been in the situation where you have to pick up some groceries, visit a friend and maybe stop by the mall or any assortment of random errands? Sadly gas isn't cheap so most likely you think to yourself, how can I do all these things while driving the shortest distance? It would be a waste of time just choosing random errand to do rather than complete each one along the way so solving the TSP is a means of figuring out what is that optimal route to do the least driving possible. From here you can easily see simple applications like a GPS routing application but it can be applied to more complex ideas like print scheduling and even satellite systems.
Genetic Algorithms
A Genetic Algorithm is a technique from the field of Machine Learning that takes inspiration from the beautiful process of evolution. I find this algorithm to be especially interesting because of how intuitive the idea is, I mean it's something that we've been a part of for countless years. How genetic algorithms work is by a taking a group of random solutions/hypotheses and putting them though stages called selection, crossover and mutation. At the end of these stages we have our hopeful new generation of solutions that go through the same process until a solution reaches a certain level of effectiveness or until the algorithm reaches a predetermined number of generations.
Lets quickly look at the steps I mentioned earlier and how my approach differs.
Initializing the Population
The beginning of the evolution process starts with a group of randomly created solutions (lets refer to the solutions as persons) which is known as the population. These randomly selected persons will be put to perform a task. This task is referred to as the fitness function and in this case the task is that each person will decide on a route to complete the TSP. The fitness function calculates the fitness of a solution, which will be the total distance travelled by that solution; in this particular problem, the smaller the fitness the better because that means a shorter distance was travelled.
Typically, genetic algorithms represent their solution as a bit-string which looks like a series of 0's and 1's.
[0 1 0 0 1 0 1 1 0 1 1 0 0 0 1]
This particular problem is not best represented as a bit-string but rather a list of the nodes / cities in the order they should be visited with the first city name as the starting city and the last city name as the final city visited (we know we must go back to the starting city so it does not need to be included twice).
[B, E, F, A, H, D, C, G]
Selection
From the initial population, each solution then has a probability to be chosen for the new population. The better the fitness, the higher the chance a solution has to be chosen. There are many selection methods each with their own formula to carry out selection and each with pros and cons. The basic selection method for genetic algorithms is called the Roulette Wheel Selection method which uses this formula
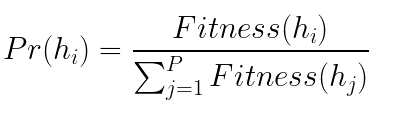
The formula may look scary but it simply calculated probability which helps us decide to take a solution or not. This models the idea of "survival of the fittest," where the better you do a task, the higher your chance of survival going into the next generation.
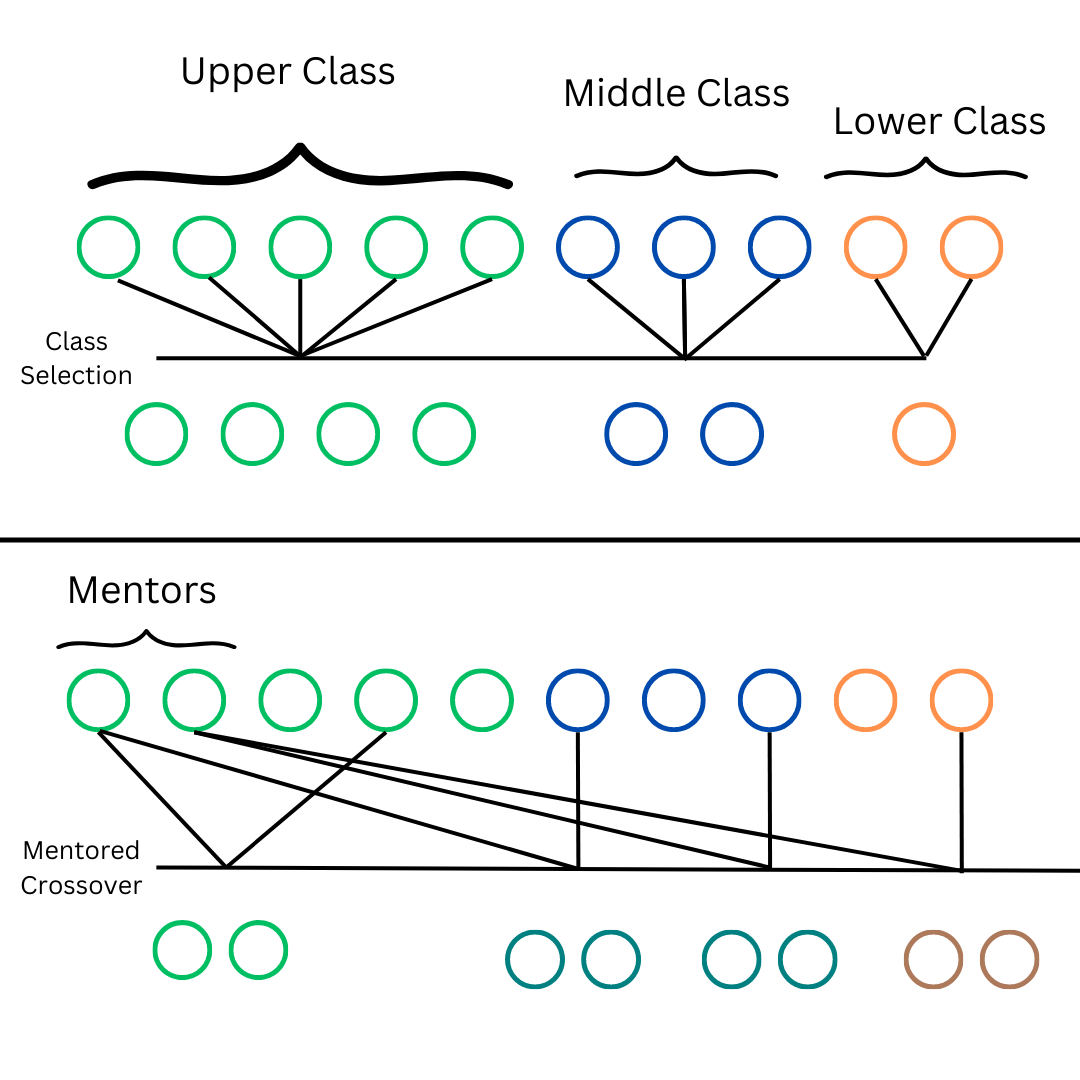
In my approach I modeled an idea I call the levelled mentorship idea. This concept takes the fitness of all the solutions but creates groups, an upper, middle and lower class where I select a large, medium and small sized group respectively. This method guarantees a high number of high performing solution while still ensuring lower class solutions are included. This makes sure the algorithm has a certain level of diversity which is important as lower performing solutions may still have great ideas within them which can be passed on to future generations.
Crossover
Crossover is the equivalent of breeding between persons and trust me when I tell you I thought for a while the best way I could word that. The crossover phase takes pairs of chosen solutions and exchanges sections of the solutions (parents) to create two new child solutions that are added to the next generation.
Rather than choosing parents only by probability, I employed both the traditional method of choosing parents by probability to reproduce and a mentorship idea where a number of solutions from the highest class will are guaranteed to be selected for crossing over and creating a new generation. This gives the diversity of allowing lower class solutions to crossover while still ensuring there is a group of high performing solutions to produce high fitness children.
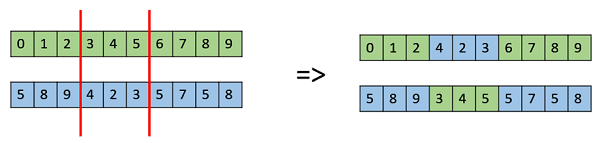
Mutation
Here we are at the final step of our evolutionary process. Mutations can occur, although rare, in evolution. Many times they can be counter productive but at times the can create a new unexplored solution that will lead to stronger generations.
Typically mutation on a bit-strings occurs by flipping a bit from a 0 to 1 or the opposite. Given that our solutions look like names of cities we can't use that same idea so instead, to mutate a solution, we swap places between two cities to change the order visited. This mutation happens very infrequently since we don't want to add too much randomness to our algorithm but can promote getting to the best solution.
The Final Result
Okay I hear you all screaming by now, "what do these solutions you've been talking about even look like!?" Well here it finally is, after running 300 solutions over 500 generations, this is what the paths look like.
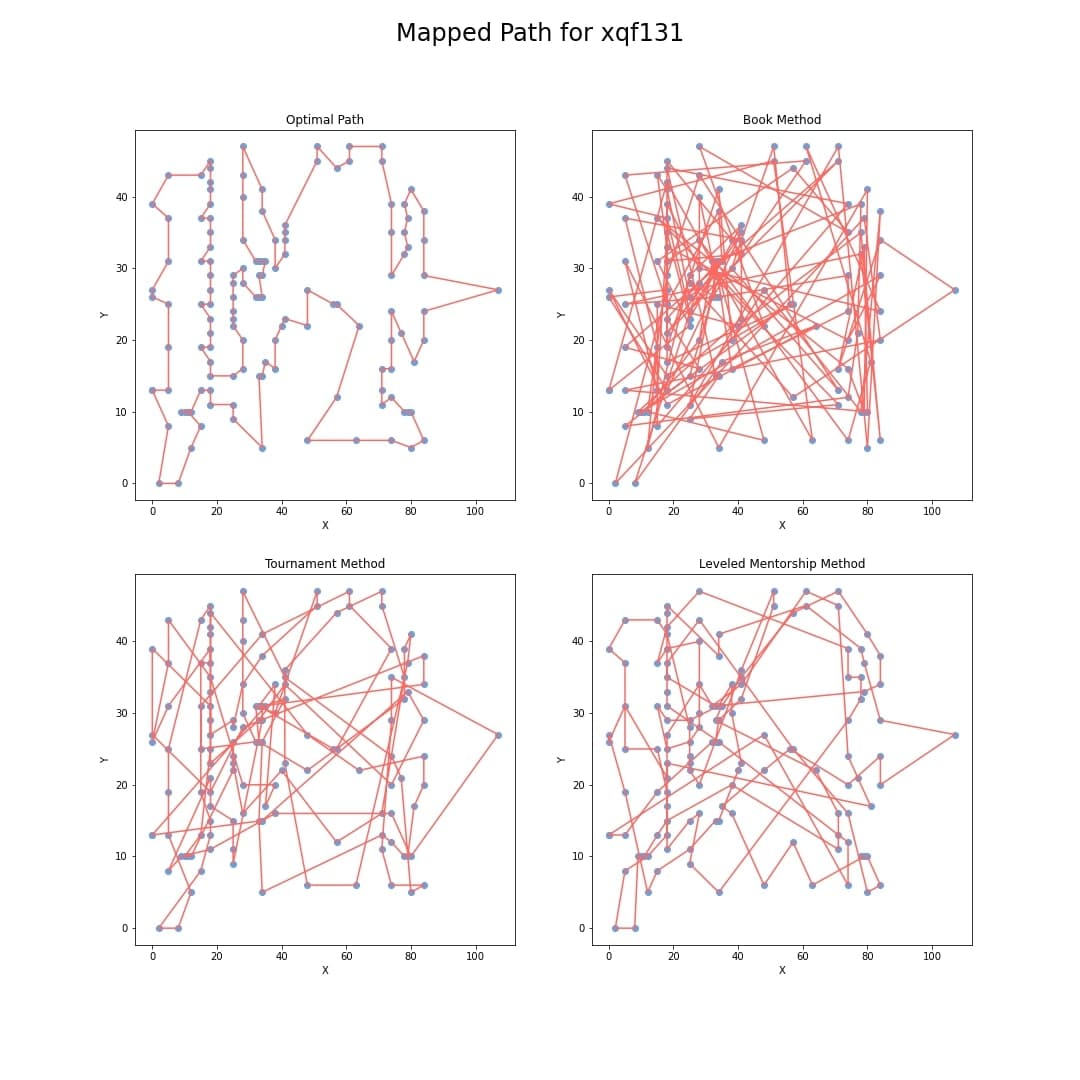
Here we have what was found to be the most optimal path by each of the methods employed with the most optimal path being in the top right, the method used by Tom Mitchel in his Machine Learning book in the top right, a method that uses the tournament selection in the bottom left and finally my beautiful creation, the levelled mentorship method in the bottom right. We see that although it isn't optimal but it keeps up with the tournament and actually does better from 2 of the 3 measurement metrics used which are the Best Fitness which is the score of the fittest individual in the generation and the Average Fitness, the average fitness of all solutions in the generation.
Conclusion
This approach doesn't come with its flaws like it's Diversity Score which was the lowest of all the approaches but what it does boast is how quickly it improves it's solution and given more generations to train the algorithm would likely find the optimal path.
This project was great to work on, the way it challenged my mind to come up with a novel approach to a method that I had only learned of that month while still being approachable and it definitely showed me how with a bit of flexibility and creativity I can approach unique and practical problems.